百科
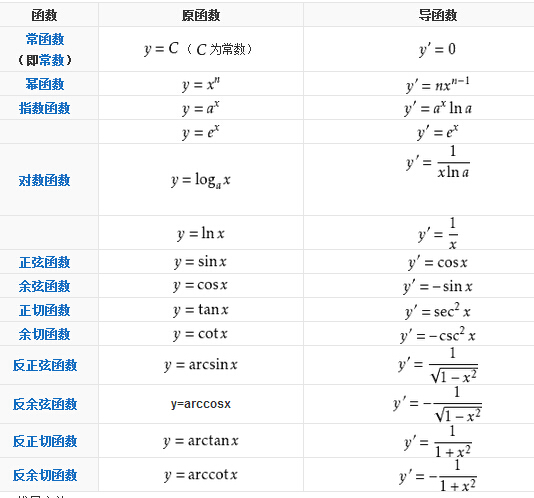
常见函数的导数
常见函数的导数
相关试题
已知  ,则
,则 ( )。
( )。已知函数  和
和 ,
,
(Ⅰ)解关于x的不等式 ;
;
(Ⅱ)求由曲线 和
和 围成的封闭图形的面积。
围成的封闭图形的面积。若连续且不恒等于的零的函数  满足
满足 ,试写出一个符合题意的函数
,试写出一个符合题意的函数 =( )。
=( )。定义在R上的可导函数f(x)满足f(-x)=f(x),f(x-2)=f(x+2),且当x∈[2,4]时,f(x)=x2+2xf′(2),则  与
与 的大小关系是
的大小关系是[ ]
A. 
B.
C.
D.不确定已知  ,则
,则 =( )。
=( )。已知f(x)在x=a处的导数值为A(A≠0),函数F(x)= f(x)-A2x2满足F′(a)=0,则aA=( )。 已知  (其中f′(x)为f(x)的导函数),则f′(1)=( )。
(其中f′(x)为f(x)的导函数),则f′(1)=( )。设函数f(x)=(x+1)ln(x+1)若对于所有的x∈(0,1),都有f′(x)≥ax成立,则实数a的取值范围是( )。 设f(x)是定义在R上的偶函数,当x>0时,f(x)+x f′(x)>0,且f(1)=0,则不等式xf(x)>0的解集为 [ ] A.(-1,0)∪(1,+∞)
B.(-1,0)∪(0,1)
C.(-∞,-1)∪(1,+∞)
D.(-∞,-1)∪(0,1)定义方程f(x)= f′(x)的实数根x0叫做函数的“新驻点”,若函数g(x)=x,h(x)=ln(x+1),φ(x)=x3-1的“新驻点”分别为α,β,  ,则α,β,
,则α,β, 的大小关系为
的大小关系为 [ ] A.α>β>

B.β>α>
C. >α>β
>α>β
D.α> >β
>β已知函数f(x)=  x2-8x,且f′(3
x2-8x,且f′(3 )=( )。
)=( )。定义方程f(x)=f′(x)的实数根叫做函数的“新驻点”,若函数g(x)=x, h(x)=ln(x+1),  (x) =x3-1的“新驻点”分别为α,β,η,则α,β,η的大小关系为
(x) =x3-1的“新驻点”分别为α,β,η,则α,β,η的大小关系为[ ] A、α>β>η
B、β>α>η
C、η>α>β
D、β>η>αy=x3+ax+1的一条切线方程为y=2x+1,则a=( )。 已知y=f(x)=ln|x|,则下列各命题中,正确的命题是 [ ] A.x>0时,f′(x)=  ;x<0时,f′(x)=
;x<0时,f′(x)=
B.x>0时,f′(x)= ;x<0时,f′(x)无意义
;x<0时,f′(x)无意义
C.x≠0时,都有f′(x)=
D.∵x=0时,f(x)无意义,∴对y=ln|x|不能求导函数f(x)=x3-x2+x+l在点(1,2)处的切线与函数g(x)=x2围成的图形的面积等于( )。 已知函数f(x)在R上满足f(x)=2f(2-x)+ex-1+x2,则曲线y=f(x)在点(1,f(1))处的切线方程是 [ ] A.2x-y-1=0
B.x-y-3=0
C.3x-y-2=0
D.2x+y-3=0设f(x)=  +xlnx,g(x)=x3-x2-3,
+xlnx,g(x)=x3-x2-3,
(Ⅰ)当a=2时,求曲线y=f(x)在x=1处的切线方程;
(Ⅱ)如果存在x1,x2∈[0,2],使得g(x1)-g(x2)≥M成立,求满足上述条件的最大整数M;
(Ⅲ)如果对任意的s,t∈[ ,2],都有f(s)≥g(t)成立,求实数a的取值范围.
,2],都有f(s)≥g(t)成立,求实数a的取值范围. 已知f(x)=x2ln(ax)(a>0).
(Ⅰ)若曲线y=f(x)在x= 处的切线斜率为3e,求a的值;
处的切线斜率为3e,求a的值;
(Ⅱ)求f(x)在 上的最小值.
上的最小值. 已知函数f(x)=x2+bx+c(b,c∈R),对任意的x∈R,恒有f′(x)≤f(x),
(Ⅰ)证明:当x≥0时,f(x)≤(x+c)2;
(Ⅱ)若对满足题设条件的任意b,c,不等式f(c)-f(b)≤M(c2-b2)恒成立,求M的最小值.f′(x)是函数f(x)=  x3+x2+3的导函数,则f′(-1)=( )。
x3+x2+3的导函数,则f′(-1)=( )。已知函数f(x)=x2+3xf′(2),则f′(2)=( )。 已知可导函数f(x)(x∈R)满足f′(x)>f(x),则当a>0时,f(a)和eaf(0)大小关系为 [ ]
A.f(a)>eaf(0)
B.f(a)<eaf(0)
C.f(a)=eaf(0)
D.f(a)≤eaf(0)已知函数f(x)在R上可导,且f(x)=x2+2x·f′(2),则f(-1)与f(1)的大小关系为 [ ]
A.f(-1)=f(1)
B.f(-1)>f(1)
C.f(-1)<f(1)
D.不确定设函数f(x)=sinx+cosx,f′(x)是f(x)的导数,若f(x)=2f′(x),则  =( )。
=( )。已知函数f(x)=ax2+bx(a≠0)的导函数f′(x)=-2x+7,数列{an}的前n项和为Sn,点P(n,Sn)(n∈N*)均在函数y=f(x)的图象上.
(1)求数列{an}的通项公式及Sn的最大值;
(2)令 ,其中n∈N*,求{nbn}的前n项和.
,其中n∈N*,求{nbn}的前n项和. f(x)与g(x)是定义在R上的两个可导函数,若f(x),g(x)满足f′(x)=g′(x),则f(x)与g(x)满足 [ ] A.f(x)=g(x)
B.f(x)=g(x)=0
C.f(x)-g(x)为常数函数
D.f(x)+g(x)为常数函数已知f1(x)=sinx+cosx,记f2(x)=f1′(x),f3(x)=f2′(x),…,fn(x)=fn-1′(x)(n∈N*,n≥2),则f1(  )+f2(
)+f2( )+…+f2 012(
)+…+f2 012( )=( )。
)=( )。求下列函数的导数.
(1)y=x2sinx;
(2)y= ;
;
(3) y=log2(2x2+3x+1).已知a为实数f(x)=(x2-4)(x-a),
(1)求导函数f′(x);
(2)若f′(-1)=0,求f(x)在[-2,2]上的最大值和最小值;
(3)若f(x)在(-∞,-2]和[2,+∞)上都是递增的,求a的取值范围。函数  的导数为( )。
的导数为( )。已知函数f(x)=sinx+ex,则f′(x)=( )。 已知函数f(x)的导函数为f′(x),且满足f(x)=3x2+2xf′(2),则f′(5)=( )。 求下列函数的导函数:
(1)y=(x-2)(x2+1);
(2) 。
。 已知f0(x)=xn,  ,其中k≤n(n,k∈N+),设F(x)=
,其中k≤n(n,k∈N+),设F(x)= ,x∈[-1,1]。
,x∈[-1,1]。
(1)写出f1(1);
(2)证明:对任意的x1,x2∈[-1,1],恒有|F(x1)-F(x2)|≤2n-1(n+2)-n-1。
最新试题
- 1名篇名句填空。1、_______________,枉用相存。_______________,心念旧恩。(《短歌行》) 2
- 2据《明史》记载:“隆庆时,诏江西烧造瓷器十余万。万历十九年命造十五万九千,既而复增八万,至三十八年未毕工。”以上材料表明
- 3“Indeed,” George Washington wrote in his diary in 1785, “som
- 4如图,已知点A(8,0),sin∠ABO=45,抛物线经过点O、A,且顶点在△AOB的外接圆上,则此抛物线的解析式为(
- 5秦始皇统一六国后,为了解决春秋战国时期诸侯国遂鹿中原.战乱不休的问题,在地方实行了,此制度也对我国行政管理产生了深远影响
- 6有人说,人的美丑并不仅仅在于他的外在的相貌如何,还在于他如何看待自己,这个观点主要说明人的美丑 [ ]A.取决
- 7恒温恒容下,将2mol A气体和2mol B气体通人体积为2 L的密闭容器中发生如下反应:2A(g)+B(g)xC(g)
- 8一位蹦床运动员仅在竖直方向上运动,弹簧床对运动员的弹力F的大小随时间t的变化规律通过传感器用计算机绘制出来,如图所示.重
- 9请阅读下面对话,根据其情景,从方框内七个选项中选出能填入下面对话的五个选项。W: May I help you?
- 10由母体通过胎盘流向胎儿的血液,其成分特点是 [ ]A.含二氧化碳较多,含氧和养料较少
热门考点
- 1阅读下面的文字,按要求回答问题。(5分)A的眼睛流出眼泪来,说:“请老太爷帮帮忙,我成家了,现下她们就在磨房里呢!她们没
- 2已知曲线C:xy-2kx+k2=0与直线l:x-y+8=0有唯一公共点,而数列{an}的首项为a1=2k,且当n≥2时点
- 3如图,△ABC是等边三角形,D为BC边上的点,∠BAD=15°,△ABD经旋转后到达△ACE的位置,那么旋转了( )A
- 4我国法律有“母法”、“子法”之分。下列选项中的两部法律,是“母法”与“子法”关系的是 [ ]A.《合同法》《反
- 5正常情况下,以下物质不属于人体内环境组成成分的是[ ]A.尿素B.抗体蛋白C.激素D.血红蛋白
- 6下图ACB为晨昏线,C为中点。图示范围仅阴影区为黑夜,其他地区为昼,据此回答1~3题。 1、C点此时地方时最晚[
- 7Robots _______ do housework instead of people in the future.
- 8It is the farm _____ we are going to pay a visit ______ prov
- 9 — What’s your favourite ________? — It’s green.A.sportB.c
- 10光辉灿烂的中华文明,以华夏文化为基础,融汇各民族文化,不断丰富发展,生生不息。 阅读材料,回答下列问题。 材料一 据《札

 ,则
,则 =
= 的导数为
的导数为



 的导数是
的导数是







 ,则
,则
 的最小值为
的最小值为



 (n∈N*)的前n项和是
(n∈N*)的前n项和是 



 x3+
x3+ x2+4x-1,其中θ∈[0,
x2+4x-1,其中θ∈[0, ],则导数f"(-1)的取值范围是
],则导数f"(-1)的取值范围是 ]
] ,6]
,6] ]
]



 的导函数是
的导函数是



 的最小值为
的最小值为
