百科

离散型随机变量及其分布列

二项分布

　　若随机变量X的分布律为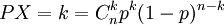 $P{X=k}=C_n^k p^k (1-p)^{n-k}$ (k=0, 1, 2, ..., n) 且0<P<1，则称X服从参数为n，P的二项分布，记作x~B(n，P)。

泊松(Poisson)分布

若随机变量X所有可能取值为0，1，2，…，它取各个值的概率为

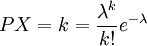　　 $P{X=k}=frac{lambda ^k}{k!} e^{- lambda}$ ，(k=0,1,2，…)

　　式中：λ > 0是常数，则称X服从参数为 λ 的泊松分布，记为X ~ Π(λ)。

相关试题

甲乙等五名大冬会志愿者被随机的分到A，B，C，D四个不同的岗位服务，每岗位至少有一名志愿者。
（1）求甲乙两人同时参加A岗位服务的概率；
（2）求甲乙两人不在同一岗位服务的概率；
（3）设随机变量为这五名志愿者中参加A岗位服务的人数，求的分布列。
题型：0103 期末题难度：| 查看答案
去年国庆期间，某商场进行促销活动，方案是：顾客消费1000元，便可获得一张奖券，每张奖券的中奖率为20％，中奖后商场返还顾客1000元。小李购买一台价格为2400元的洗衣机，只能获得两张奖券，于是小李补偿50元给同事购买600元的上衣一件，可以获得3张奖券，记小李抽奖后的实际开支为元。
（1）求的分布列；
（2）试说明小李出资50元便增加一张奖券是否划算？
题型：0103 模拟题难度：| 查看答案

设随机变量X的分布列为

题型：0103 期末题难度：| 查看答案

题型：0103 期中题难度：| 查看答案

题型：0103 模拟题难度：| 查看答案

-1

1-2a

车间地上放有一批大小相同的黄、白两种颜色的乒乓球，黄、白数量之比为1：2，现从车间中每次任意取出一个球，若取出的是黄球则结束，若取出的是白球，则将其放回箱中，并继续从箱中任意取出一个球，但取球的次数最多不超过n次，以ξ表示取球结束时已取到白球的次数。
（Ⅰ）求ξ的分布列；
（Ⅱ）求ξ的数学期望。

桌面上有三颗均匀的骰子（6个面上分别标有数字1，2，3，4，5，6）。重复下面的操作，直到桌面上没有骰子：将骰子全部抛掷，然后去掉那些朝上点数为奇数的骰子。记操作三次之内（含三次）去掉的骰子的颗数为X。
（Ⅰ）求P（X=1）；
（Ⅱ）求X的分布列及期望EX。

某射手射击所得环数X的分布列如下：

题型：浙江省期末题难度：| 查看答案

题型：江苏模拟题难度：| 查看答案

题型：江苏高考真题难度：| 查看答案

题型：广东省高考真题难度：| 查看答案

题型：浙江省高考真题难度：| 查看答案

题型：江苏高考真题难度：| 查看答案

题型：天津高考真题难度：| 查看答案

题型：四川省高考真题难度：| 查看答案

题型：广东省高考真题难度：| 查看答案

题型：江西省高考真题难度：| 查看答案

0.1

0.3

一个暗箱中有大小相同的3只白球和2只黑球共5只球，每次从中取出1只球，取到白球得2分，取到黑球得3分，甲从暗箱中有放回地依次取出3只球．
(Ⅰ)写出甲总得分ξ的分布列；
(Ⅱ)求甲总得分ξ的期望Eξ。

某工厂生产甲、乙两种产品，甲产品的一等品率为80%，二等品率为20%；乙产品的一等品率为90%，二等品率为10%。生产1件甲产品，若是一等品则获得利润4万元，若是二等品则亏损1万元；生产1件乙产品，若是一等品则获得利润6万元，若是二等品则亏损2万元。设生产各件产品相互独立。
（Ⅰ）记x（单位：万元）为生产1件甲产品和1件乙产品可获得的总利润，求X的分布列；
（Ⅱ）求生产4件甲产品所获得的利润不少于10万元的概率。

为了解甲、乙两厂的产品质量，采用分层抽样的方法从甲、乙两厂生产的产品中分别抽出取14件和5件，测量产品中的微量元素x，y的含量（单位：毫克）。下表是乙厂的5件产品的测量数据：

（1）已知甲厂生产的产品共有98件，求乙厂生产的产品数量；
（2）当产品中的微量元素x，y满足x≥175，且y≥75时，该产品为优等品。用上述样本数据估计乙厂生产的优等品的数量；
（3）从乙厂抽出上述5件产品中，随机抽取2件，求抽取的2件产品中优等品数ξ的分布列极其均值（即数学期望）。

如图，一个小球从M处投入，通过管道自上而下落到A或B或C。已知小球从每个叉口落入左右两个管道的可能性是相等的．某商家按上述投球方式进行促销活动，若投入的小球落到A，B，C，则分别设为1，2，3等奖，
(Ⅰ)已知获得1，2，3等奖的折扣率分别为50%，70%，90%。记随机变量ξ为获得k(k=1，2，3)等奖的折扣率，求随机变量ξ的分布列及期望Eξ；
(Ⅱ)若有3人次(投入1球为1人次)参加促销活动，记随机变量η为获得1等奖或2等奖的人次，求P(η=2)．

在1，2，3，…，9这9个自然数中，任取3个数。
（1）求这3个数中恰有1个是偶数的概率；
（2）记ξ为这3个数中两数相邻的组数（例如：若取出的数为1，2，3，则有两组相邻的数1，2和2，3，此时ξ的值是2）。求随机变量ξ的分布列及其数学期望Eξ。

某工厂生产甲、乙两种产品．甲产品的一等品率为80%，二等品率为20%；乙产品的一等品率为90%，二等品率为10%。生产1件甲产品，若是一等品则获得利润4万元，若是二等品则亏损1万元；生产1件乙产品，若是一等品则获得利润6万元；若是二等品则亏损2万元．设生产各件产品相互独立，
(Ⅰ)记X(单位：万元)为生产1件甲产品和1件乙产品可获得的总利润，求X的分布列；
(Ⅱ)求生产4件甲产品所获得的利润不少于10万元的概率。

在10件产品中，有3件一等品，4件二等品，3件三等品，从这10件产品中任取3 件，求：
（1）取出的3件产品中一等品件数X的分布列和数学期望；
（2）取出的3件产品中一等品件数多于二等品件数的概率。

某种有奖销售的饮料，瓶盖内印有“奖励一瓶”或“谢谢购买”字样，购买一瓶若其瓶盖内印有“奖励一瓶”字样即为中奖，中奖概率为

，甲、乙、丙三位同学每人购买了一瓶该饮料，
(Ⅰ)求甲中奖且乙、丙都没有中奖的概率；
(Ⅱ)求中奖人数ξ的分布列及数学期望Eξ。

随机抽取某厂的某种产品200件，经质检，其中有一等品126件、二等品50件、三等品20件、次品4件．已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元，而1件次品亏损2万元．设1件产品的利润（单位：万元）为ξ，
（1）求ξ的分布列；
（2）求1件产品的平均利润（即ξ的数学期望）；
（3）经技术革新后，仍有四个等级的产品，但次品率降为1%，一等品率提高为70%．如果此时要求1件产品的平均利润不小于4.73万元，则三等品率最多是多少？

某饮料公司招聘一名员工，现对其进行一项测试，以便确定工资级别。公司准备了两种不同的饮料共8杯，其颜色完全相同，并且其中4杯为A饮料，另外4杯为B饮料，公司要求此员工一一品尝后，从8杯饮料中选出4杯A饮料.若4杯都选对，则月工资定为3500元；若4杯选对3杯，则月工资定为2800元；否则月工资定为2100元。令X表示此人选对A饮料的杯数，假设此人对A和B两种饮料没有鉴别能力，
（1）求X的分布列；
（2）求此员工月工资的期望。

某农场计划种植某种新作物，为此对这种作物的两个品种（分别称为品种甲和品种乙）进行田间试验。选取两大块地，每大块地分成n小块地，在总共2n小块地中，随机选n小块地种植品种甲，另外n小块地种植品种乙。
（1）假设n=4，在第一大块地中，种植品种甲的小块地的数目记为X，求X的分布列和数学期望；
（2）试验时每大块地分成8小块，即n=8，试验结束后得到品种甲和品种乙在个小块地上的每公顷产量（单位：kg/hm²）如下表：

题型：辽宁省高考真题难度：| 查看答案

题型：贵州省模拟题难度：| 查看答案

题型：0128 模拟题难度：| 查看答案

题型：0127 模拟题难度：| 查看答案

题型：模拟题难度：| 查看答案

题型：同步题难度：| 查看答案

品种甲

403

397

390

404

388

400

412

406

品种乙

419

403

412

418

408

423

400

413

中华人民共和国《道路交通安全法》中将饮酒后违法驾驶机动车的行为分成两个档次；“酒后驾车”和“醉酒驾车”，其检测标准是驾驶人员血液中的酒精含量Q（简称血酒含量，单位是毫克/100毫升），当20≤Q≤80时，为酒后驾车；当Q＞80时，为醉酒驾车，某市公安局交通管理部门于2011年2月的某天晚上8点至11点在市区设点进行一次拦查行动，共依法查出了60名饮酒后违法驾驶机动车者，如图为这60名驾驶员抽血检测后所得结果画出的频率分布直方图（其中Q≥140的人数计入120≤Q＜140人数之内）。
（1）求此次拦查中醉酒驾车的人数；
（2）从违法驾车的60人中按酒后驾车和醉酒驾车利用分层抽样抽取8人做样本进行研究，再从抽取的8人中任取3人，求3人中含有醉酒驾车人数X的分布列和期望。

袋中有同样的球5个，其中3个红色，2个黄色，现从中随机且不返回地摸球，每次摸1个，当两种颜色的球都被摸到时，即停止摸球，记随机变量ξ为此时已摸球的次数，求：
（1）随机变量ξ的概率分布；
（2）随机变量ξ的数学期望与方差。

甲，乙两人进行围棋比赛，约定每局胜者得1分，负者得0分，比赛进行到有一人比对方多2分或打满6局时停止。设甲在每局中获胜的概率为p（p>

），且各局胜负相互独立。已知第二局比赛结束时比赛停止的概率为

。
（1）求p的值；
（2）设ξ 表示比赛停止时已比赛的局数，求随机变量ξ 的分布列和数学期望Eξ 。

经选拔，某同学获得了参加A、B、C三所大学的自主招生考试的资格，已知某同学选择参加A大学测试而不选择B和C大学的概率为0.16，选择参加A和B大学测试而不选择C大学的概率为0.24，三所大学都不被选择的概率为0.4。假设该同学选择参加哪所大学测试互不影响。用ξ表示该同学选择的大学个数与未选大学个数之差。
（1）求ξ的分布列与数学期望；
（2）记“关于x的方程|x|-ξx=1有负根而无正根”为事件W，求事件W发生的概率P（W）。

有甲、乙两个盒子，甲盒中有6张卡片，其中2张写有数字0，2张写有数字1，2张写有数字2；乙盒中也有6张卡片，其中3张写有数字0，2张写有数字1，1张写有数字2，如果从甲盒中取1张卡片，乙盒中取2张卡片，设取出的3张卡片数字之积为随机变量ξ，
(1)求ξ的分布列和数学期望；
(2)记“函数f(x)=sin(2x+

ξ)，按向量a=(

，0)平移后得到一条对称轴为x=

的函数g(x)”为事件A，求事件A发生的概率．

下列4个表格中，可以作为离散型随机变量分布列的一个是

若随机变量X的分布列如下表，

题型：同步题难度：| 查看答案

已知随机变量X的分布列为P（X=k）=

，k=1，2，…，则P（2＜X≤4）等于（）

若随机变量X的分布列为P（X=i）=

（i=1，2，3），则P（X=2）=（）

一盒中有12个乒乓球，其中9个新的，3个旧的，从盒中任取3个球来用，用完后装回盒中，此时盒中旧球个数X是一个随机变量，其分布列为P（X=i）=p_i，i=1，2，…，6，则P（X=4）的值为( )

已知随机变量X的概率分布如下表：

题型：同步题难度：| 查看答案

题型：专项题难度：| 查看答案

题型：湖北省模拟题难度：| 查看答案

设随机变量X只能取5，6，7，…，16这12个值，且取每个值的概率相同，则P（X＞8）=（），P（6＜X≤14）=（）。

设某项试验的成功率为失败率的2倍，用随机变量X去描述1次试验的成功次数，则P（X=0）的值为（）。

设S是不等式x²-x-6≤0的解集，整数m，n∈S。
（1）记“使得m+n=0成立的有序数组（m，n）”为事件A，试列举A包含的基本事件；
（2）设ξ=m²，求ξ的分布列及其数学期望E（ξ）。

下列表中能成为随机变量的分布列的是（）

A、

B、

C、

D、

盒子中放了10个乒乓球，其中8个是新球，2个是旧球（即至少用过一次的球）．每次比赛，都拿出其中2个球用，用完后全部放回，
(Ⅰ)设第一次比赛取出的两个球中新球的个数为ξ，求随机变量ξ的分布列和数学期望；
(Ⅱ)求第二次比赛任取2球都是新球的概率。

随机变量ξ的概率分布规律为P（ξ=n）=a

（n=1，2，3，4，…），其中a是常数，则P（

）的值为

已知随机变量的概率分布如下：

题型：辽宁省高考真题难度：| 查看答案

题型：安徽省高考真题难度：| 查看答案

题型：高考真题难度：| 查看答案

题型：辽宁省高考真题难度：| 查看答案

题型：安徽省高考真题难度：| 查看答案

题型：山东省高考真题难度：| 查看答案

题型：安徽省高考真题难度：| 查看答案

题型：辽宁省高考真题难度：| 查看答案

题型：湖北省高考真题难度：| 查看答案

题型：湖南省高考真题难度：| 查看答案

题型：江西省高考真题难度：| 查看答案

题型：高考真题难度：| 查看答案

题型：辽宁省高考真题难度：| 查看答案

题型：重庆市高考真题难度：| 查看答案

题型：湖北省高考真题难度：| 查看答案

最新试题

热门考点

	1	2	3	4	5	6	7	8	9	10
P										m
在添加剂的搭配使用中，为了找到最佳的搭配方案，需要对各种不同的搭配方式作比较。在试制某种牙膏新品种时，需要选用两种不同的添加剂。现有芳香度分别为0，1，2，3，4，5的六种添加剂可供选用。根据试验设计原理，通常首先要随机选取两种不同的添加剂进行搭配试验。用ξ表示所选用的两种不同的添加剂的芳香度之和，（Ⅰ）写出ξ的分布列；（以列表的形式给出结论，不必写计算过程）（Ⅱ）求ξ的数学期望Eξ。（要求写出计算过程或说明道理）
某批产品成箱包装，每箱5件，一用户在购进该批产品前先取出3箱，再从每箱中任意抽取2件产品进行检验，设取出的第一、二、三箱中分别有0件、1件、2件二等品，其余为一等品，（Ⅰ）用ξ表示抽检的6件产品中二等品的件数，求ξ的分布列及ξ的数学期望；（Ⅱ）若抽检的6件产品中有2件或2件以上二等品，用户就拒绝购买这批产品，求这批产品被用户拒绝购买的概率。
现有甲、乙两个项目，对甲项目每投资十万元，一年后利润是1.2万元、1.18万元、1.17万元的概率分别为、、；已知乙项目的利润与产品价格的调整有关，在每次调整中价格下降的概率都是p（0＜p＜1），设乙项目产品价格在一年内进行2次独立的调整，记乙项目产品价格在一年内的下降次数为ξ，对乙项目每投资十万元，ξ取0、1、2时，一年后相应利润是1.3万元、1.25万元、0.2万元。随机变量ξ₁、ξ₂分别表示对甲、乙两项目各投资十万元一年后的利润。（1）求ξ₁、ξ₂的概率分布和数学期望Eξ₁、Eξ₂；（2）当Eξ₁＜Eξ₂时，求p的取值范围。
在医学生物学试验中，经常以果蝇作为试验对象，一个关有6只果蝇的笼子里，不慎混入了两只苍蝇（此时笼内共有8只蝇子：6只果蝇和2只苍蝇），只好把笼子打开一个小孔，让蝇子一只一只地往外飞，直到两只苍蝇都飞出，再关闭小孔.以ξ表示笼内还剩下的果蝇的只数。（1）写出ξ的分布列（不要求写出计算过程）；（2）求数学期望Eξ；（3）求概率P（ξ≥Eξ）。
甲、乙两队参加奥运知识竞赛，每队3人，每人回答一个问题，答对者对本队赢得一分，答错得零分。假设甲队中每人答对的概率均为，乙队中3人答对的概率分别为，且各人回答正确与否相互之间没有影响，用ξ表示甲队的总得分。（1）求随机变量ξ的分布列和数学期望；（2）用A表示“甲、乙两个队总得分之和等于3”这一事件，用B表示“甲队总得分大于乙队总得分”这一事件，求P（AB）。
为防止风沙危害，某地决定建设防护绿化带，种植杨树、沙柳等植物，某人一次种植了n株沙柳，各株沙柳成活与否是相互独立的，成活率为p，设ξ为成活沙柳的株数，数学期望Eξ=3，标准差σξ为。（1）求n，p的值并写出ξ的分布列；（2）若有3株或3株以上的沙柳未成活，则需要补种，求需要补种沙柳的概率。
某地有A、B、C、D四人先后感染了甲型H1N1流感，其中只有A到过疫区，B肯定是受A感染的。对于C，因为难以判定他是受A还是受B感染的，于是假定他受A和受B感染的概率都是，同样也假设D受A、B和C感染的概率都是。在这种假定之下，B、C、D中直接受A感染的人数X就是一个随机变量，写出X的分布列（不要求写出计算过程），并求X的均值（即数学期望）。
某人向一目射击4次，每次击中目标的概率为。该目标分为3个不同的部分，第一、二、三部分面积之比为1：3：6。击中目标时，击中任何一部分的概率与其面积成正比。（1）设X表示目标被击中的次数，求X的分布列；（2）若目标被击中2次，A表示事件“第一部分至少被击中1次或第二部分被击中2次”，求P（A）。
一个盒子里装有4张大小形状完全相同的卡片，分别标有数2，3，4，5；另一个盒子也装有4张大小形状完全相同的卡片，分别标有数3，4，5，6，现从一个盒子中任取一张卡片，其上面的数记为x；再从另一盒子里任取一张卡片，其上面的数记为y，记随机变量η=x+y，求η的分布列和数学期望。
某城市有甲、乙、丙3个旅游景点，一位客人游览这三个景点的概率分别是0.4，0.5，0.6，且客人是否游览哪个景点互不影响，设ξ表示客人离开该城市时游览的景点数与没有游览的景点数之差的绝对值。（1）求ξ的分布及数学期望；（2）记“函数f（x）=x²-3ξx+1在区间[2，+∞）上单调递增”为事件A，求事件A的概率。
A、B两位同学各有五张卡片，现以投掷均匀硬币的形式进行游戏，当出现正面朝上时A赢得B一张卡片，否则B赢得A一张卡片。规定掷硬币的次数达9次时，或在此前某人已赢得所有卡片时游戏终止，设ξ表示游戏终止时掷硬币的次数，（1）求ξ的取值范围；（2）求ξ的数学期望Eξ。
甲、乙两队进行一场排球比赛．根据以往经验，单局比赛甲队胜乙队的概率为0.6，本场比赛采用五局三胜制，即先胜三局的队获胜，比赛结束。设各局比赛相互间没有影响，令ξ为本场比赛的局数，求ξ的概率分布和数学期望。（精确到0.0001）
已知随机变量ξ的概率分布如下，则P（ξ=10）=

[ ]
A. B. C. D.
设一汽车在前进途中要经过4个路口，汽车在每个路口遇到绿灯（允许通行）的概率为，遇到红灯（禁止通行）的概率为。假定汽车只在遇到红灯或到达目的地才停止前进，ξ表示停车时已经通过的路口数，求：（1）ξ的概率的分布列及期望Eξ；（2）停车时最多已通过3个路口的概率。
设随机变量ξ的概率分布为P（ξ=k）=，a为常数，k=1，2，…，则a=（）。