百科
直线的倾斜角与斜率
直线斜率的定义
斜率,亦称“角系数”,表示一条直线相对于横轴的倾斜程度。一条直线与某平面直角坐标系横轴正半轴方向的夹角的正切值即该直线相对于该坐标系的斜率。 如果直线与x轴垂直,直角的正切值无穷大,故此直线不存在斜率。 当直线L的斜率存在时,对于一次函数y=kx+b(斜截式),k即该函数图像(直线)的斜率。
由一条直线与右边X轴所成的角的正切。
k=tanα=(y2-y1)/(x2-x1)
直线的倾斜角
平面直角坐标系中,对于一条与X轴相交的直线,如果把X轴绕着交点按逆时针方向旋转到和直线重合时所转的最小正角记为α,则α叫做直线的倾斜角.
规定:当直线和X轴平行或重合时,直线倾斜角为0º,所以,倾斜角的范围是0º《α《180º.
直线的斜率公式
直线的斜率公式:
给定两点P1(x1,y1),P2(x2,y2),x1≠x2,如何用两点的坐标来表示直线P1P2的斜率?
斜率公式:
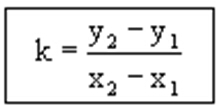
对于上面的斜率公式要注意下面四点:
(1) 当x1=x2时,公式右边无意义,直线的斜率不存在,倾斜角α= 90°, 直线与x轴垂直;
(2)k与P1、P2的顺序无关, 即y1,y2和x1,x2在公式中的前后次序可以同时交换, 但分子与分母不能交换;
(3)斜率k可以不通过倾斜角而直接由直线上两点的坐标求得;
(4) 当 y1=y2时, 斜率k = 0, 直线的倾斜角α=0°,直线与x轴平行或重合.
(5)求直线的倾斜角可以由直线上两点的坐标先求斜率而得到.
相关试题
设点A(2,﹣3),B(﹣3,﹣2),直线l过点P(1,1)且与线段AB相交则l的斜率k的取值范围 [ ] A.k≥  或k ≤﹣4
或k ≤﹣4
B. ≤k≤4
≤k≤4
C.﹣4≤k≤
D.k≥4或k≤﹣
已知圆的方程为x2+y2﹣6x﹣8y=0,设圆中过点(2,5)的最长弦与最短弦分别为AB、CD,则直线AB与CD的斜率之和为( ). 已知θ∈R,则直线  的倾斜角的取值范围是( )
的倾斜角的取值范围是( )若图中的直线l1、l2、l3的斜率分别为k1、k2、k3,则( ) A.k1<k2<k3 B.k2<k1<k3 C.k3<k2<k1 D.k1<k3<k2 “龟兔赛跑”讲述了这样的故事:领先的兔子看着慢慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点…,用S1、S2分别表示乌龟和兔子所行的路程,t为时间,则下图与故事情节相吻合的是( ) A. 
B. 
C. 
D. 
若a>0,b<0,直线y=ax+b的图象可能是( ) A. 
B. 
C. 
D. 
对于直线l的倾斜角α与斜率k,下列说法错误的是( ) A.α的取值范围是[0°,180°) B.k的取值范围是R C.k=tanα D.当α∈(90°,180°)时,α越大k越大 已知两直线的方程分别为l1:x+ay+b=0,l2:x+cy+d=0,它们在坐标系中的位置如图所示( ) A.b>0,d<0,a<c B.b>0,d<0,a>c C.b<0,d>0,a<c D.b<0,d>0,a>c 直线l1:y=ax+b,l2:y=bx+a (a≠0,b≠0,a≠b),在同一坐标系中的图形大致是( ) A. 
B. 
C. 
D. 
直线y=
x的倾斜角为______.3 若方程Ax+By+C=0表示与两条坐标轴都相交的直线,则( ) A.A≠0B≠0C≠0 B.A≠0B≠0 C.B≠0C≠0 D.A≠0C≠0 在下列四个命题中,正确的共有( )
①坐标平面内的任何一条直线均有倾斜角和斜率;
②直线的倾斜角的取值范围是[0,π];
③若一条直线的斜率为tanα,则此直线的倾斜角为α;
④若一条直线的倾斜角为α,则此直线的斜率为tanα.A.0个 B.1个 C.2个 D.3个 如图,直线l1,l2,l3的斜率分别为k1,k2,k3,则( ) A.k1>k2>k3 B.k3>k2>k1 C.k2>k1>k3 D.k3>k1>k2 若图中的直线l1,l2,l3的斜率分别为k1,k2,k3,则( ) A.k1<k2<k3 B.k3<k1<k2 C.k3<k2<k1 D.k1<k3<k2 如图所示,设k1,k2,k3分别是直线l1,l2,l3的斜率,则( ) A.k1<k2<k3 B.k3<k1<k2 C.k3<k2<k1 D.k1<k3<k2 若图中的直线l1,l2,l3的斜率为k1,k2,k3则( ) A.k1<k2<k3 B.k3<k1<k2 C.k2<k1<k3 D.k3<k2<k1 若两直线l1,l2的倾斜角分别为α1,α2,则下列四个命题中正确的是( ) A.若α1<α2,则两直线斜率k1<k2 B.若α1=α2,则两直线斜率k1=k2 C.若两直线斜率k1<k2,则α1<α2 D.若两直线斜率k1=k2,则α1=α2 如图,若直线l1,l2,l3的斜率分别为k1,k2,k3,则k1,k2,k3三个数从小到大的顺序依次是______. 
“龟兔赛跑”讲述了这样的故事:领先的兔子看着慢慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点…,用S1、S2分别表示乌龟和兔子所行的路程,t为时间,则下图与故事情节相吻合的是( ) A. 
B. 
C. 
D. 
设a>0,f(x)=ax2+bx+c,曲线y=f(x)在点P(x0,f(x0))处切线的倾斜角的取值范围为[0,
],则P到曲线y=f(x)对称轴距离的取值范围为( )π 4 A.[0,
]1 a B.[0,
]1 2a C.[0,|
|]b 2a D.[0,|
|]b-1 2a 直线l只经过第一、三、四象限,则直线l的斜率k( ) A.大于零 B.小于零 C.大于零或小于零 D.以上结论都有可能 若图中的直线l1、l2、l3的斜率分别为k1、k2、k3,则( ) A.k1<k2<k3 B.k2<k1<k3 C.k3<k2<k1 D.k1<k3<k2 
直线y=
x-1的倾斜角是( )3 3 A.30° B.120° C.60° D.150° 直线x+
y+5=0的倾斜角是( )3 A.30° B.120° C.60° D.150° 已知线段AB两个端点A(2,-3),B(-3,-2),直线l过点P(1,2)且过线段AB相交,则l的斜率k的取值范围为______. 过两点A(3,
+1),B(2,1)的直线l的倾斜角为______.3 已知直线l的方程为x-y-a2=0(a≠0),则下列叙述正确的是( ) A.直线不经过第一象限 B.直线不经过第二象限 C.直线不经过第三象限 D.直线不经过第四象限 已知直线l的斜率的绝对值等于
,则直线的倾斜角为( )3 A.60° B.30° C.60°或120° D.30°或150° 在直角坐标系中,直线y+1=0的倾斜角α的大小是______弧度. 已知直线px+qy-1=0(p,q∈R)经过第二、三、四象限,则p,q满足的条件是______. 直线
x-y+2=0的倾斜角的大小为( )3 A.30° B.60° C.120° D.150° 直线x+y-1=0不可能通过( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 对于直线l的倾斜角α与斜率k,下列说法错误的是( ) A.α的取值范围是[0°,180°) B.k的取值范围是R C.k=tanα D.当α∈(90°,180°)时,α越大k越大 已知两直线的方程分别为l1:x+ay+b=0,l2:x+cy+d=0,它们在坐标系中的位置如图所示( ) A.b>0,d<0,a<c B.b>0,d<0,a>c C.b<0,d>0,a<c D.b<0,d>0,a>c 
直线l的方程是y=x-1,则该直线l的倾斜角为( ) A.30°w B.45° C.60° D.135° 过点(-3,0)和点(-4,
)的直线的倾斜角是( )3 A.30° B.150° C.60° D.120° 已知直线ax+by+c=0不经过第二象限,且ab<0,则( ) A.c>0 B.c<0 C.ac≥0 D.ac≤0 已知角θ的顶点与原点重合,始边与x轴的正半轴重合,终边在直线y=2x上,则cos2θ=( ) A.- 4 5 B.- 3 5 C. 3 5 D. 4 5 已知a,b,c是两两不等的实数,则经过两点A(a,c)和B(b,c)的直线的倾斜角是 ______. 若直线l经过点P(2,3)且与两坐标轴围城一个等腰直角三角形,则直线l的方程为______或______. 直线l:xsinθ+y+1=0(θ∈R)的倾斜角α的取值范围是______. 已知直线l的方程为y=-x+1,则该直线l的倾斜角为( ) A.30° B.45° C.60° D.135° 直线l经过原点和点(1,
),则直线l的倾斜角为( )3 A.30° B.45° C.60° D.120° 已知θ∈R,则直线xsinθ-
y+1=0的倾斜角的取值范围是( )3 A.[0°,30°] B.[150°,180°) C.[0°,30°]∪[150°,180°) D.[30°,150°] 直线x=1的倾斜角和斜率分别是( ) A.45°,1 B.135°,-1 C.90°,不存在 D.180°,不存在 直线ax+by+c=0同时要经过第一、二、四象限,则a,b,c应满足( ) A.ab>0,bc<0 B.ab<0,bc>0 C.ab>0,bc>0 D.ab<0,bc<0 若直线mx+ny+p=0通过第一、二、三象限,则( ) A.mn>0,np>0 B.mn<0,np<0 C.mn>0,np<0 D.mn<0,np>0 最新试题- 1珠江三角洲发展基塘农业的有利条件是[ ]A、地势低平,河网密布,降水充沛B、赤道从北部穿过,适宜种植热带经济作物
- 2张家界国际乡村音乐周活动中,来自中、日、美的三名音乐家准备在同一节目中依次演奏本国的民族音乐,若他们出场先后的机会是均等
- 3下图示人体血液循环的一部分,箭头为血液方向。请据图判断,血管P和Q分别是( )A.动脉、静脉B.静脉、动脉 C.静脉
- 4下列诗句横线上应填的修饰语,最富于表现力的一项是[ ] 大堰河,含泪的去了!/同着___的人世生活的凌侮,/同
- 5有三种金属元素a、b、c,在相同条件下,b的最高价氧化物的水化物的碱性比a的最高价氧化物的水化物的碱性强;a可以从c的盐
- 6近年来,我市推动“生态城市”建设取得明显成效。走在林荫大道上,人们感到空气特别清新和湿润。从生物学角度看,空气清新湿润主
- 7物体沿一直线单向运动,第一秒内通过5m,第二秒内通过10m,第三秒内通过24m后停下,则后两秒内的平均速度为 m
- 8明末思想家黄宗羲被尊为“中国思想启蒙之父”,他的思想主要反映在《明夷待访录》中。“明夷”本为《周易》中的一卦,“明”即是
- 9起重机保持的不变功率P=10kw,将地面上质量为m=500kg的物体由静止向上吊起h=2m,并刚好达到最大速度。(g取1
- 10边长为1cm的正六边形面积等于 cm2.
热门考点- 1下图为太平洋大洋环流系统的一部分,读图回答1~2题。 1、该图位于[ ]A、北半球B、南半球C、东半球D、西半球
- 2完形填空。 I have a good friend. 1 name is Lisa. She comes
- 3如图所示,试在电池组、电压表和电流表中,任选两件填入电路的空缺处,使电灯L1和L2能同时发光.
- 4社会保障直接关系着百姓的切身利益,是全面建设小康社会,构建社会主义和谐社会的重要内容。以德国为代表的市场经济模式也非常强
- 5一次函数y=ax+b的图像如图所示,则下面结论中正确的是[ ]A.a<0,b<0B.a<0,b>0C.a>0,b
- 62008年1月8日,国务院下发《关于限制生产销售使用塑料购物袋的通知》,塑料购物袋已成为白色污染的主要来源。自2008年
- 7图中共有线段______条.
- 8The global financial crisis (金融危机) has made many people ____
- 9下面哪项措施的目的是为了减慢水的蒸发( )A.用电热吹风机将湿头发吹干B.用扫帚把地面的积水向周围扫开C.将水果用保鲜
- 10下列句子翻译有误的一项是[ ]A、饥冻虽切,违己交病:饥寒虽然来得急迫,但是违背自己本意去做官,身体就会得病。
版权所有 CopyRight © 2012-2019 超级试练试题库 All Rights Reserved.









 在第二象限内,则直线
在第二象限内,则直线 不经过的象限为
不经过的象限为