线段的计算

　　线段是几何中最基本的概念，是同学们最先接触到的简单图形，也是学习三角形、四边形的基础，熟练掌握线段的计算方法，是七年级所学内容的重点和难点之一。下面介绍几种线段的计算方法，供同学们参考。

　　一、利用几何的直观性求两线段差

　　例1. 如图1，A、B、C、D是直线l上的顺次四点，且线段AC=5，BD=4，则线段AB-CD等于__________。

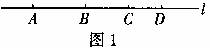
　　分析：观察图形可知：AB=AC-BC，CD=BD-BC，根据已知条件通过已知线段AC=5，BD=4，即可求出AB-CD。

　　解：因为AB=AC-BC，CD=BD-BC，

　　所以AB-CD=(AC-BC)-(BD-BC)=AC-BD=5-4=1，故填1。

　　点评：本题所考查的知识主要是线段的和、差的概念，关键在于应用线段差进行计算，本题图形中的点较多，当线段上点较多时，要逐个进行分析，而不要混在一起无法理出线索。

　　二、利用线段中点的性质求线段长

　　例2. 如图2，已知线段AB=80cm，M为AB的中点，P在MB上，N为PB的中点，且NB=14cm，求PA的长。

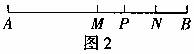
　　分析：从图形可以看出，线段AP等于线段AM与MP的和，也等于线段AB与PB的差，所以，欲求线段PA的长，只要能求出线段AM与MP或者求出线段PB的长即可。

　　解：因为N是PB的中点，NB=14，所以PB=2NB=2

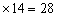(cm)。

　　又因为AP=AB-PB，AB=80，所以AP=80-28=52(cm)。

　　点评：在几何计算中，要结合图形中已知线段和所求线段的位置关系求解，要做到步步有根据。

　　三、利用分类讨论图形的多样性求线段长

　　例3. 已知线段AB=8cm，在直线AB上画线段BC，使它等于3cm，则线段AC的长是_______。

　　分析：线段AB是固定不变的，而直线上线段BC的位置与C点的位置有关，C点可以在线段AB上，也可以在线段AB的延长线上。

　　解：本题主要考查分类讨论的数学思想方法。

　　(1)若点C在线段AB上，如图3(1)，

　　因为AB=8cm，BC=3cm，

　　所以AC=AB-BC=8-3=5(cm);

　　(2)若点C在线段AB的延长线上，如图3(2)，

　　因为AB=8cm，BC=3cm，

　　所以AC=AB+BC=8+3=11(cm)。

　　所以线段AC的长为5cm或11cm。

　　点评：解本题时，有些同学往往只考虑其中一种情况，而导致漏解，这主要是没有充分理解“在直线AB上画线段BC”这句话的确切含义。

　　综上所述，解决线段的计算问题，除选择适当的方法外，观察图形、掌握几何图形的多样性是关键，同时还要注意规范书写格式等。